Hypothesis Testing in Statistics
At times, the magnitudes of various statistics, trick us into believing that some relation between the variables exists, when the truth is these observations emerge only due to random chance causes.
Now, certainly, since these relations exist only due to chance and not due to any logical reason, we get tricked into believing another side of the story than what the data wishes to convey. The solution to these problems in data analysis was solved when hypothesis testing was first introduced into the statistical world.
Test of significance is a process where we test the validity of our claims using experimental evidence. These sophisticated methods are used to validate and examine whether a specific empirical evidence is due to chance or because there lies a plausible explanation to it.
These claims could be various types. In statistics, these claims are called hypothesis. There are two hypothesis, one Null hypothesis (H0) another Alternative hypothesis (H1). Technical meaning being H0 represents a theory that has been put forward, either because it is believed to be true or because it is to be used as a basis for argument, but has not been proved. And H1 represents the contradictory statement to H0, which is claimed against H0.

Theoretically speaking, the hypothesis can be formed of the following types: two tailed or single tailed. Lets understand this with an example based on the testing for significance of the correlation coefficients between two variables in the dataset.
- Two-tailed hypothesis testing
Here, suppose the sample correlation coefficient between two variables, say A and B, is equal to 0.598. Now, in order to check if this is purely due to chance or is there actually any relation between the variables, we set the following hypothesis:
H0: The correlation coefficient between A and B is insignificant, i.e., the population correlation coefficient between these variables is equal to zero or there is no correlation.
H1: The correlation coefficient between A and B is significant, i.e., the population correlation coefficient between these variables is not equal to zero or there is some correlation.
This is a two-tailed hypothesis testing, since, we reject the null hypothesis or H0 when the empirical evidence indicates that the estimate of the population correlation coefficient between A and B is either significantly positive (lies to the right of zero, in the number line) or is significantly negative (lies to the left of zero), in other words, is not equal to zero.

2. Single-tailed hypothesis testing
Here, our alternative hypothesis could be of the form, < or >, this means that, we reject the null hypothesis only when the value significantly lies to only side of the value (either < or >), for instance,
H0: The correlation coefficient between A and B is insignificant, i.e., the population correlation coefficient between these variables is equal to zero or there is no correlation.
H1: The correlation coefficient between A and B is significant and negative, i.e., the population correlation coefficient between these variables is less than zero.
This is a single-tailed hypothesis testing, since, we reject the null hypothesis or H0 when the empirical evidence indicates that the estimate of the population correlation coefficient between A and B lies significantly to the left of zero (is significantly negative for us to assume that the correlation is actually negative).
Further topic of Discussion
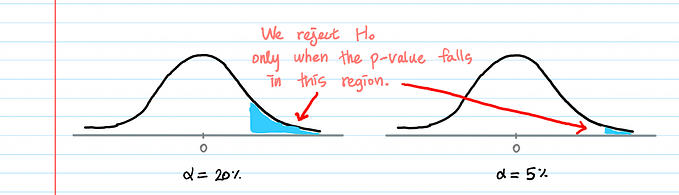
In statistics, no fact is legitimate without factual-data-heavy evidence, even the testing of these hypothesis requires some statistical tools and methods. We know different statistics follow different statistical distributions, there are methods of testing their significance, for example, testing the significance of the population mean is done differently under certain specifications than testing for the significance of the population correlation coefficients or population variances. These test statistics are used to obtain the p-value for the hypothesis testing which are further used to conclude the claims based on some level of significance (or alpha).

Now that we understand the need and types of hypothesis, our next step is to understand the terminology in hypothesis testing. This would help us scrutinize the graph better hence aiding in a comprehensive understanding. Follow me to to stay updated with the content that follows :)